Die Lichtgeschwindigkeit ist eine der wichtigsten Naturkonstanten. Mit ihrer Kenntnis läßt sich eine absolute Aussage über die Größe des Universums machen. Man denke dabei z.B. an die Angaben der Entfernungen in Lichtjahren. Doch wie hat man eigentlich herausgefunden, wie schnell das Licht ist? Mit dieser Geschichte sind viele hochrangige Astronomen und Wissenschaftler verbunden.

Galileo Galilei (1564 – 1642)

Der erste Versuch, die Lichtgeschwindigkeit zu bestimmen, geht auf das Allroundgenie Galilei zurück, der diesen im Alter von gerade mal 17 Jahren durchführte. Dazu leuchtete er mit einer abdunkelbaren Lampe einen Helfer auf einem mehrere Kilometer entfernten Berg an, der sofort nach Erreichen des Lichtsignales seine Lampe einschalten sollte. Die Zeit vom Aussenden des Lichtstrahles Galileis bis zum Sichtbarwerden des Gegensignales sollte unter Berücksichtigung der menschlichen Reaktionszeit eine gewisse Zeit benötigen, wenn das Licht sich nicht mit unendlich großer Geschwindigkeit ausbreitet. Allerdings bekam Galilei immer nur Werte heraus, die im Bereich dieser Reaktionszeiten lag, sodaß er schlußfolgerte, die Lichtgeschwindigkeit ist zu groß für seine Methode.

Ole Rømer (1644 – 1710)

Wie allgemein bekannt ist, wird der Jupiter von einigen Monden umrundet. Da die Jupiterbahn nicht allzuweit von der Ekliptik abweicht, kommt es regelmäßig zu Vorübergängen, Verfinsterungen und Bedeckungen der Galileischen Monde. Ole Rømer beobachtete 1675 die Verfinsterungen des Mondes Io, die etwa alle 42,5 Stunden eintreten. Kennt man also die Dauer bis zur nächsten Verfinsterung, dann kann man wunderbare Vorhersagen machen. Das machte auch Rømer und merkte schnell, daß diese mit der Zeit mehr und mehr abwichen. Beispielhaft seien an dieser Stelle aus visuellen Gründen die Bedeckungsanfänge Ios vom 19.4. und 28.7.2005 dargestellt (Bild 1). Natürlich lassen sich diese nicht beobachten, da der Jupiterschatten vorher den Mond verdeckt.

Bild 1:
links: Bedeckungsanfang von Io am 19.4.2005 um 1:58 MESZ
Mitte: der vorhergesagte Bedeckungsanfang am 28.7.2005 um 22:18 MESZ erweist sich als falsch
rechts: der tatsächliche Bedeckungsanfang ist erst um 22:28 MESZ Man beachte zudem den deutlichen Größenunterschied der Jupiterscheibe, ein deutlicher Beweis dafür, daß er am 28.7. viel weiter weg stand als am 19.4.

Am 19.4. war der Bedeckungsanfang für Io 1:58 MESZ. Nach 104 Perioden würde man den Bedeckungsanfang am 28.7. um 22:18 erwarten. Er tritt jedoch erst etwa 10 Minuten später ein. Woran liegt das?
Nun: Die Zeit für eine Jupiterumrundung hat sich natürlich nicht verändert. Rømer merkte schnell, daß es nur an der Endlichkeit der Lichtgeschwindigkeit liegen kann. Da sich die Planeten mit unterschiedlichen Winkelgeschwindigkeiten um die Sonne bewegen, verändern sich natürlich auch deren gegenseitige Abstände. So betrug der Abstand des Jupiters zur Erde am 19.4. circa 4,5 Astronomische Einheiten, am 28.7. jedoch etwa 5,75 AE. Die Verzögerung von 10 Minuten liegt also darin begründet, daß das Licht für die 1,2 AE mehr Strecke diese Zeit benötigt. Durch anschließende geometrische Betrachtungen schloß Rømer daraus, daß das Licht 22 Minuten benötigt, um den Erdbahndurchmesser zu durchlaufen. Da drei Jahre zuvor die Astronomische Einheit zu 139 Mio. km bestimmt worden war, war erstmals eine Größenordnung der Lichtgeschwindigkeit gefunden, die mit etwa 250.000 km/s für die damaligen Mittel sehr gut war (Anm.: da die A.E. etwa 10 Mio. km zu klein angenommen wurde, entspricht der Wert Rømers heute etwa 227.000 km/s).
Dieser Werte wurden durch Cassini (14 min bzw. 357.000 km/s) und Halley (17 min bzw. 294.000 km/s) noch verbessert.

James Bradley (1692 – 1762)

Im Jahre 1725 stellte Bradley zusammen mit Molyneux Beobachtungen des Sternen ? Dra an, mit dem Ziel, dessen Parallaxe zu bestimmen. Damit sollte eine Aussage über die Entfernung des Sternes möglich sein. Über geometrische Beziehungen müsste ? Dra eigentlich am 3.12 seinen südlichsten Punkt erreichen und anschließend wieder nach Norden wandern. Diesen Gefallen tat ihnen der Stern aber nicht. Er bewegte sich noch ein Vierteljahr weiter Richtung Süden, insgesamt mehr als 20“ weit. Weitere Sternbeobachtungen lieferten das gleiche grundlegende Ergebnis, jedoch mit anderen Werten. Bradley stand vor einem scheinbar unlösbaren Rätsel. Wie so oft half auch hier der Zufall weiter. Auf einer Schiffsreise im Jahre 1728 bemerkte Bradley, daß die Wetterfahne bei jedem Kurswechsel eine andere Richtung anzeigte als zuvor. Die angezeigte Richtung ist eine Vektoraddition aus der Fahrtgeschwindigkeit des Schiffes und der Windgeschwindigkeit. Sie kann gleichsam auf den Sternenhimmel übertragen werden: Die Windgeschwindigkeit entspricht der Lichtgeschwindigkeit und die Fahrtgeschwindigkeit des Bootes derjenigen der Erde. Diese Erkenntnis trug er 1729 der Royal Society vor. Mit der Kenntnis der Bahngeschwindigkeit der Erde und dem gemessenen Winkel ergibt sich dann die Lichtgeschwindigkeit.

Formelmäßig sieht das so aus:

c = v_Erde / tan α (1)

c = Lichtgeschwindigkeit
v_Erde = Bahngeschwindigkeit der Erde (etwa 29,7 km/s)
α = ermittelte Aberration eines Sternes, der genau senkrecht zur Bahnbewegung der Erde steht (also auf dem ekliptikalen Nord- oder Südpol); α = 20’’48

Als Nebenprodukt der Aberration folgt zudem, daß die Sterne viel weiter weg sind, als ursprünglich angenommen, da ja ein beträchtlicher Teil der beobachteten Parallaxen auf die Aberration fällt.

Armand Hippolyte Louis Fizeau (1819 – 1896)

Nachdem nun zwei astronomische Methoden erfolgreich die Endlichkeit der Lichtgeschwindigkeit bewiesen und einen groben Richtwert gegeben hatten, versuchte man nach über hundert Jahren der Stagnation, diese mit erdgebundenen Methoden zu ermitteln. Den ersten Versuch startete der französische Physiker Fizeau in den Jahren 1849/50 mit einem von Arago vorgeschlagenen Versuch. Der Versuch wird auch als Zahnradmethode oder Zahnradversuch bezeichnet (Bild 2). Man schickt Licht durch ein schnell rotierendes Zahnrad auf einen entfernt liegenden Spiegel, welcher das Licht zurückwirft.

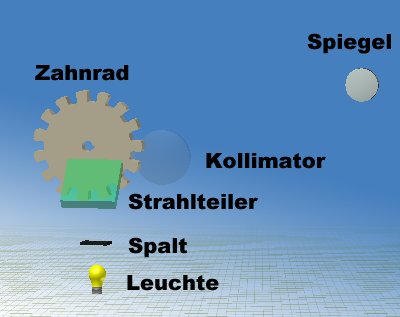
Bild 2:
Aufbau des Zahnradversuches nach Fizeau

Dabei gibt es nun mehrere Fälle:

1. Die Drehgeschwindigkeit des Zahnrades ist noch so klein, daß man den reflektierten Strahl durch die gleiche Lücke des Zahnrades sehen kann.
2. Die Drehgeschwindigkeit ist so groß, daß das reflektierte Licht an dem der Lücke folgenden Zahn hängenbleibt.
3. Die Drehgeschwindigkeit des Zahnrades ist so groß, daß der reflektierte Strahl durch die nächste Lücke scheint.

c = 4 ⋅ s ⋅ z ⋅ n (2)

wobei

c = Lichtgeschwindigkeit
s = Abstand Zahnrad – Reflektor
z = Zähnezahl des Zahnrades
n = Drehzahl des Zahnrades

kann man dann auf die Lichtgeschwindigkeit schließen (Formel gilt für Fall 2).
Fizeau folgerte daß die Lichtgeschwindigkeit etwa 295.000 km/s beträgt.

Jean Bernard Léon Foucault (1819 – 1868)

Wenig später verbesserte der unter Spiegelschleifern wohlbekannte französische Physiker Foucault das Verfahren.
Mit seinem Drehspiegelversuch (Bild 3), der im Aufbau bis auf das Zahnrad identisch mit demjenigen von Fizeau ist, konnte er die Lichtgeschwindigkeit noch besser ermitteln. Hierbei wird das Licht nach der Reflektion an einem Polygonspiegel auf einen Reflektor geschickt und gelangt zurück auf den Drehspiegel, der sich aber schon ein Stückchen weitergedreht hat. Es ergibt sich eine Winkelabweichung, die gemessen und ausgewertet werden kann (siehe Bild 2).

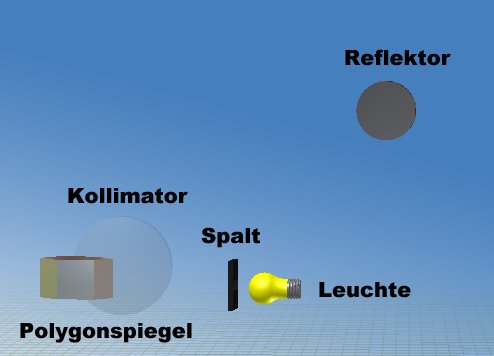
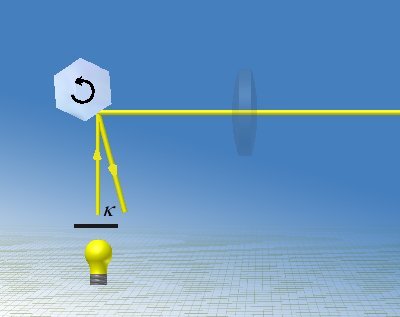
Bild 3:
oben: Aufbau des Drehspiegelversuches nach Foucault
unten: Da sich der Spiegel ein Stück weitergedreht hat, während der Strahl zum Reflektor und wieder zurück läuft, wird der Strahl nicht in sich zurückgeworden, sondern seitlich um den Winkel κ abgelenkt

Es besteht folgender mathematischer Zusammenhang:

c = 2 ⋅ π ⋅ n ⋅ AS_n / 15 ⋅ κ (3)

Dabei sind:

c = Lichtgeschwindigkeit
n = Drehzahl des Polygonspiegels
AS_n = Strecke vom Auftreffpunkt des Lichtstrahles auf den Polygonspiegel zum Reflektorspiegel
κ = gemessener Winkel vom eintretenden zum austretenden Lichtstrahl

Über einfachste mathematische Beziehungen errechnete Foucault eine Lichtgeschwindigkeit von etwa 298.000 km/s.

Albert Abraham Michelson (1852 – 1931)

Er trieb den Drehspiegelversuch mit den Jahren zum Exzeß. Dazu benutzte er deutlich bessere Optiken und viel längere Meßstrecken. Damit kam er dem heute gültigen Wert für die Lichtgeschwindigkeit immer näher. Sein um 1890 gefundener Wert von c = (299.853 ± 60) km/s blieb für 45 Jahre der Standardwert. Erst 1924 verbesserte sich dieser nochmals, als er eine Meßstrecke von über 70 km aufbaute. Diese war auf 5cm genau ausgemessen (ohne LASER oder GPS!!!). Allerdings gab es zuvor bei diesem Projekt viele Schwierigkeiten, z.B. durch Erdbeben und Waldbrände. Hierbei fand er eine Lichtgeschwindigkeit von c = (299.796 ± 6) km/s. Dies sollte sein bester Wert bleiben.
Mitten in neuen Meßreihen in einer evakuierten Röhre von 1,6 km Länge starb er. Diese Meßreihen brachten später einen schlechteren Wert, nämlich c = (299.774 ± 11) km/s.

Die Festlegung der Lichtgeschwindigkeit.

Schon zu Michelsons Zeiten konnte die Lichtgeschwindigkeit auf elektrischen und elektrooptischen Wegen ohne solch großen Aufwand bestimmt werden.
Den besten Wert erreichte Evenson im Jahre 1972. Er bestimmte c zu 299.792,46 km/s. Im Jahre 1983 wird die Vakuum-Lichtgeschwindigkeit schließlich auf den noch heute gültigen Wert c = 299.792,458 km/s festgelegt. Dieser weist eine relative Unsicherheit von 4*10-9 (entspricht etwa 12 cm) auf.

Danksagung

Ich danke Herrn Dr. Bernd Pfeiffer für richtigstellende Hinweise.

Literatur

[1] Paturi, F.R.; „Harenberg Schlüsseldaten Astronomie“, Dortmund: Harenberg Lexikon Verlag in der Heidelberg Kommunikation Verlags- und Mediengesellschaft mbH & Co. KG
[2] Zimmermann, H.; „Lexikon der Astronomie“, 8. Auflage, Heidelberg, Berlin: Spektrum Akademischer Verlag
[3] Herrmann, J.; „Das große Lexikon der Astronomie“, München: Orbis Verlag für Publizistik GmbH